
这样的问题可以通过改进程序加以解决,就上面这个程序而言,只要在计算Y坐标时采用四舍五入的方法取整就能很好地解决这个问题。然而这样做并不是最理想的改进方法,因为这个程序还有其它一些缺点:比如我们将程序中的续止点X、Y坐标交换一下,即由(200,1)变成(1,200),那么这个程序就会产生十分尴尬的结果:整条线变成了两个点。看来"弱智"也是这个程序的一个缺陷。它至少应该能对(Y1-Y0)和(X1-X0)这两个差值做些比较,如果(Y1-Y0) (X1-X0)那么程序应该以(Y1-Y0)作为循环计数,而采用公式X=Y/K计算X坐标。
列举了以上一些不足之处,意在说明采用公式"Y=Kx+b"来画直线并不适用于计算机。其实上述这些缺点都是次要因素,最主要的一个缺点就是这种算法要使用乘法和除法运算。乘除法运算要消耗大量的时间,所以说这种算法是极低效的,这是这种算法的致命的缺陷。因此我们必须设计出既有效率又有效果的画线算法。
当我们给出一条直线的两个端点后,比如起点为(0,0),终点为(5,2),屏幕上应该显示出什么样的图形才能给人感觉是一条直线呢?毫无疑问,屏幕上应该显示出如图8-4(a)所示的几个点,即每画两个点之后Y坐标值要加1。如果起点仍为(0,0),终点为(11,3),那么屏幕显示出的图形就应该如图8-4(b)所示的样子了。不难看出如果我们所设计的程序能够在画第3、5点(对于图8-4b来说是画第3、7、11点)时自动将Y坐标值加上1,那么就能产生另人满意的效果来。看来要解决的一个关键问题就是要判断在什么样的情况下所画点的Y坐标值需要加1。
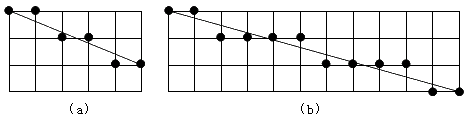
图9-4 直线的近似画法
第一个问题比较好解决,从图中我们可以看到,直线的起点A(0,0)的ΔYa=0,第二个点B的ΔYb=0+K,第三个点C的ΔYc=0+K+K,第四个点D的ΔYd=0+K+K+K-1,第五个点E的ΔYe=0+K+K+K+K-1,以此类推,其中的K就是这条直线的斜率,K=ΔY'/ΔX'=(Y1-Y0)/(X1-X0)。可以看出计算ΔY的过程都包括一个"斜率累加"的过程,只是在Y坐标值加1之后要从累加值中减去1。如果我们把K=ΔY'/ΔX'代入公式,则有ΔYa=0,ΔYb=ΔY'/ΔX',ΔYc=(ΔY'+ΔY')/ΔX',ΔYd=(ΔY'+ΔY'+ΔY'-ΔX')/ΔX',"斜率累加"就变成"ΔY'累加"了。
由ΔY的计算式我们还可以看出每个点的ΔY都是分数,那么如何判断一个分数是否大于1/2呢?很明显若一个分数满足"(分子x2)>分母",则这个分数就大于1/2。对于图中的B点而言,如果2ΔY'>ΔX',就说明其ΔY大于1/2。对于C点,如果2ΔY'+2ΔY'>ΔX',则其ΔY大于1/2。而D