| -252- | PC机汇编语言实战精解 |  |
|||||||||||||||||||
| 点就更麻烦一些，当2ΔY'+ΔY'+2ΔY'-2ΔX'>ΔX'时其ΔY值是大于1/2的。从这样一个判断的过程中我们能近一步发现在计算ΔY时真正需要累加的既不是"K"，也不是"ΔY'"，而是"2ΔY'"。 | |||||||||||||||||||||
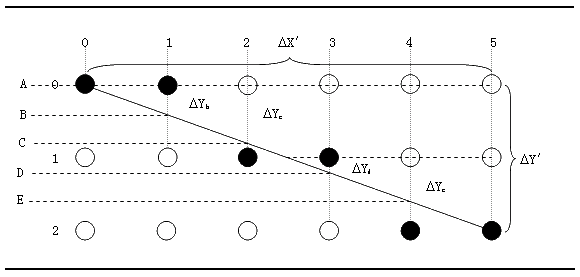
 图9-5 决定最近点的算法 |
|||||||||||||||||||||
| 对于图中这条直线，线上各点有如表9-2这样的计算结果： | |||||||||||||||||||||
| 表9-2 决定最近点的计算实例 | ΔY'=2，ΔX'=5，2ΔY'=4，2ΔX'=10 | ||||||||||||||||||||
| 点 | 2ΔY'的累加值 | 累加值与ΔX'比较 | 实际点的坐标值 | 累加值调整 | |||||||||||||||||
| A | 0 | (0,0) | |||||||||||||||||||
| B | 0+4=4 | 4<5 | (1,0) | ||||||||||||||||||
| C | 4+4=8 | 8>5 | (2,1) | 8-10=-2 | |||||||||||||||||
| D | -2+4=2 | 2<5 | (3,1) | ||||||||||||||||||
| E | 2+4=6 | 6>5 | (4,2) | 6-10=-4 | |||||||||||||||||
| F | -4+4=0 | 0<5 | (5,2) | ||||||||||||||||||
|
通过以上计算，我们清楚地看到当表中第三栏内出现">"时，实际所画点的Y坐标值都加上了1，同时2 Y 的累加值根据2 X 作了相应调整。而在整个过程之中X坐标值始终都是递增的。 这个画线算法是由一位名为Bresenham的程序员首创，因此这个算法被命名为Bresenham算法。因为" 2"的操作可以由左移位代替，所以在这个算法中实际上是没有乘法、除法运算的，因而这个算法十分快速，这是其最突出的优点，也是它长盛不衰的原因。 程序LOVE.ASM演示了Bresenham直线算法的一种应用，这个程序有些复杂，它将屏幕中央连续画6个封闭的多边形，由这些多边形组成一个图案。 |
|||||||||||||||||||||
|
LOVE.ASM start_x start_y data assume dotbuff |
equ equ segment ds:data dw dw |
100 0 26h 48h,09h,42h,0dh,3ch,11h, |
；起点X坐标 ；起点Y坐标 ；第一部分总的点数 37h,14h,31h,16h,29h,18h,28h,19h,2eh,1ah |
||||||||||||||||||
| Copyright © 2004-2015 Reanimator | www.cookmoon.org | ||||||||||||||||||||